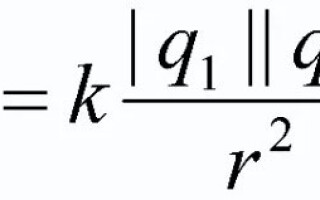Định luật Coulomb, định nghĩa và công thức - điện tích điểm và tương tác của chúng

Giữa các vật thể tích điện có một lực tương tác do đó chúng có thể hút hoặc đẩy nhau. Định luật Coulomb mô tả lực này, cho thấy mức độ tác dụng của nó, tùy thuộc vào kích thước và hình dạng của chính vật thể đó. Quy luật vật lý này sẽ được thảo luận trong bài viết này.

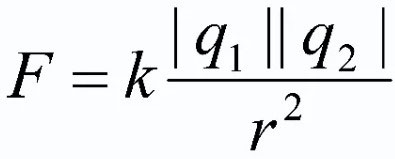
Công thức định luật Coulomb.

Nội dung

1 Phí điểm tĩnh
2 Cân bằng xoắn của Charles Coulomb
3 Hệ số tỷ lệ k và hằng số điện
4 Phương của lực Coulomb và dạng vectơ của công thức
5 Trường hợp luật Coulomb được áp dụng trong thực tế
6 Hướng của các lực trong định luật Coulomb
7 Lịch sử phát hiện ra luật

Phí điểm tĩnh

Định luật Coulomb áp dụng cho các vật thể đứng yên nhỏ hơn nhiều so với khoảng cách của chúng với các vật thể khác. Một điện tích điểm được tập trung trên các vật thể như vậy. Khi giải quyết các vấn đề vật lý, kích thước của các cơ quan được coi là bị bỏ qua, bởi vì chúng không thực sự quan trọng.

Trong thực tế, các điện tích điểm ở trạng thái dừng được mô tả như sau:

Điểm mang điện tích dương q1. Điểm mang điện tích dương q2.

Trong trường hợp này q₁ và q₂ - đây là tích cực điện tích và lực Coulomb tác dụng lên chúng (không được thể hiện trong hình). Kích thước của các tính năng điểm không quan trọng.

Ghi chú! Các khoản phí còn lại nằm ở một khoảng cách nhất định với nhau, trong các bài toán thường được ký hiệu bằng chữ cái r. Hơn nữa trong bài báo, các điện tích này sẽ được xem xét trong môi trường chân không.

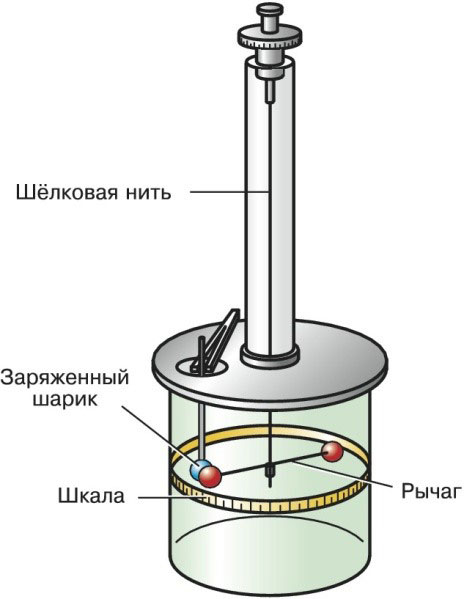
Cân bằng xoắn của Charles Coulomb

Thiết bị này, được Coulomb phát triển vào năm 1777, giúp suy ra sự phụ thuộc của lực sau này được đặt theo tên ông. Với sự trợ giúp của nó, sự tương tác của các điện tích điểm, cũng như các cực từ, được nghiên cứu.

Cân bằng xoắn có một sợi tơ nhỏ nằm trong mặt phẳng thẳng đứng, từ đó treo một đòn cân bằng. Phí điểm nằm ở hai đầu của đòn bẩy.

Dưới tác dụng của ngoại lực, đòn bẩy bắt đầu chuyển động theo phương ngang. Cần sẽ chuyển động trong mặt phẳng cho đến khi nó được cân bằng bởi lực đàn hồi của sợi chỉ.

Trong quá trình chuyển động, đòn bẩy lệch với trục tung một góc nhất định. Nó được coi là d và được gọi là góc quay. Biết giá trị của thông số này, có thể tìm được mômen của các lực phát sinh.

Đọc thêm: Dòng điện trong những từ đơn giản là gì

Cân bằng lực xoắn của Charles Coulomb trông như thế này:

Cân bằng lực xoắn của Charles Coulomb.

Hệ số tỷ lệ k và hằng số điện 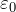$\ varepsilon_0$

Trong công thức của định luật Coulomb có tham số k - hệ số tỉ lệ hoặc $\ varepsilon_0$ là hằng số điện. Hằng số điện $\ varepsilon_0$ được trình bày trong nhiều sách tham khảo, sách giáo khoa, Internet, và nó không cần phải đếm! Hệ số tỷ lệ chân không dựa trên $\ varepsilon_0$ có thể được tìm thấy bằng công thức nổi tiếng:

$k = \ frac {1} {4 \ cdot \ pi \ cdot \ varepsilon_0}$

Nơi đây $\ varepsilon_0 = 8,85 \ cdot 10 ^ {- 12} \ frac {C ^ 2} {H \ cdot m ^ 2}$ là hằng số điện,

$\ pi = 3,14$ - Số Pi,

$k = 9 \ cdot 10 ^ {9} \ frac {H \ cdot m ^ 2} {C ^ 2}$ là hệ số tỉ đối trong chân không.

Thông tin thêm! Nếu không biết các tham số trình bày ở trên, nó sẽ không có tác dụng tìm lực tương tác giữa hai điện tích điểm.
Lập công thức và công thức của định luật Coulomb

Để tóm tắt những điều trên, cần đưa ra công thức chính thức của định luật tĩnh điện chính. Nó có dạng:

Lực tương tác của hai điện tích điểm nằm yên trong chân không tỷ lệ thuận với tích của các điện tích này và tỷ lệ nghịch với bình phương khoảng cách giữa chúng. Hơn nữa, sản phẩm của các khoản phí phải được thực hiện theo mô-đun!

$F = k \ cdot \ frac {| q_1 | \ cdot | q_2 |} {r ^ 2}$

Trong công thức này q₁ và q₂là các điện tích điểm, được coi là vật thể; r² - khoảng cách trên mặt phẳng giữa các vật thể này, tính theo hình vuông; k là hệ số tương xứng ( $9 \ cdot 10 ^ {9} \ frac {H \ cdot m ^ 2} {C ^ 2}$ đối với chân không).

Phương của lực Coulomb và dạng vectơ của công thức

Để hiểu đầy đủ về công thức, bạn có thể hình dung định luật Coulomb:

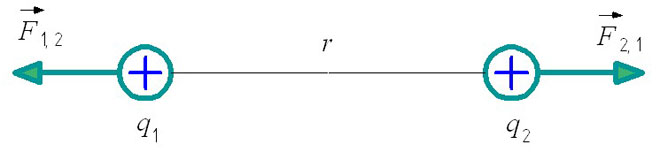
Phương của lực Coulomb đối với hai điện tích điểm cùng cực.

F_1,2- lực tương tác của điện tích thứ nhất đối với điện tích thứ hai.

F_2,1- Lực tương tác của điện tích thứ hai so với điện tích thứ nhất.

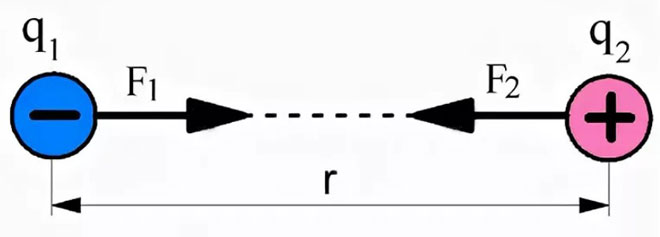
Ngoài ra, khi giải các bài toán về tĩnh điện, cần phải tính đến một quy tắc quan trọng: các điện tích cùng tên đẩy, và các điện tích trái dấu thì hút. Vị trí của các lực tương tác trong hình phụ thuộc vào điều này.

Nếu coi các điện tích trái dấu thì lực tương tác của chúng sẽ hướng về nhau, mô tả lực hút của chúng.

Hướng của lực Coulomb đối với hai điện tích điểm có cực khác nhau.

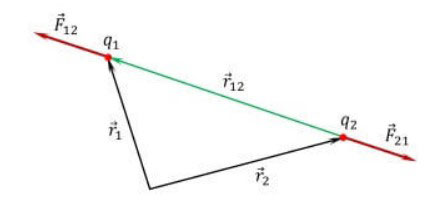
Công thức của định luật cơ bản của tĩnh điện ở dạng vectơ có thể được biểu diễn như sau:

$\ vec F_1_2 = \ frac {1} {4 \ cdot \ pi \ cdot \ varepsilon_0} \ cdot \ frac {q_1 \ cdot q_2} {r_1_2 ^ 3} \ cdot \ vec r_1_2$

$\ vec F_1_2$ là lực tác dụng lên điện tích điểm q1, tính từ mặt của điện tích q2,

$\ vec r_1_2$ là vectơ bán kính nối điện tích q2 với điện tích q1,

Đọc thêm: Làm thế nào để làm một bảng mạch in điện tử tại nhà?

$r = | \ vec r_1_2 |$

Quan trọng! Sau khi viết công thức dưới dạng vectơ, lực tương tác của hai điện tích điểm sẽ cần được chiếu lên trục để đặt các dấu hiệu một cách chính xác. Hành động này là một hình thức và thường được thực hiện trong tinh thần mà không có bất kỳ ghi chú nào.

Trường hợp luật Coulomb được áp dụng trong thực tế

Định luật cơ bản của tĩnh điện là khám phá quan trọng nhất của Charles Coulomb, định luật này đã được tìm thấy ứng dụng của nó trong nhiều lĩnh vực.

Các tác phẩm của nhà vật lý nổi tiếng đã được sử dụng trong quá trình phát minh ra các thiết bị, dụng cụ, bộ máy khác nhau. Ví dụ, một cột thu lôi.

Với sự trợ giúp của cột thu lôi, các tòa nhà dân cư và tòa nhà được bảo vệ khỏi sét khi có giông bão. Như vậy, mức độ bảo vệ của các thiết bị điện được tăng lên.

Cột thu lôi hoạt động theo nguyên tắc sau: trong cơn giông, các điện tích cảm ứng mạnh dần dần tích tụ trên mặt đất, chúng bốc lên và bị hút vào các đám mây. Trong trường hợp này, một điện trường khá lớn được hình thành trên mặt đất. Gần cột thu lôi, điện trường trở nên mạnh hơn, do đó điện tích hào quang được đánh lửa từ đầu thiết bị.

Hơn nữa, điện tích hình thành trên mặt đất bắt đầu bị thu hút bởi điện tích của đám mây có dấu hiệu ngược lại, vì nó phải theo định luật Charles Coulomb. Sau đó, không khí trải qua quá trình ion hóa, và cường độ điện trường trở nên nhỏ hơn ở gần cuối cột thu lôi. Do đó, nguy cơ sét đánh vào tòa nhà là tối thiểu.

Ghi chú! Nếu tòa nhà được lắp đặt cột thu lôi, thì sẽ không có lửa và tất cả năng lượng sẽ đi vào lòng đất.

Dựa trên định luật Coulomb, một thiết bị được gọi là "Máy gia tốc hạt" đã được phát triển và đang có nhu cầu lớn ngày nay.

Trong thiết bị này, một điện trường mạnh được tạo ra, làm tăng năng lượng của các hạt rơi vào nó.

Hướng của các lực trong định luật Coulomb

Như đã đề cập ở trên, hướng của lực tương tác của hai điện tích điểm phụ thuộc vào cực của chúng. Những thứ kia. Các điện tích cùng tên sẽ đẩy lùi và các điện tích trái dấu sẽ thu hút.

Đọc thêm: Cách chế tạo máy dò kim loại bằng tay của chính bạn, trợ giúp cho người mới bắt đầu

Lực Coulomb cũng có thể được gọi là vectơ bán kính, bởi vì chúng được định hướng dọc theo đường kẻ giữa chúng.

Trong một số bài toán vật lý, người ta đưa ra các vật thể có hình dạng phức tạp, không thể sử dụng cho một điện tích điểm, tức là bỏ qua kích thước của nó. Trong tình huống này, cơ thể đang được xem xét phải được chia thành nhiều phần nhỏ và mỗi phần phải được tính toán riêng biệt, sử dụng định luật Coulomb.

Các vectơ lực thu được bằng cách tách được tổng hợp theo các quy tắc của đại số và hình học. Kết quả là lực tạo thành, sẽ là câu trả lời cho vấn đề này. Phương pháp giải này thường được gọi là phương pháp tam giác.

Hướng của các vectơ lực Coulomb.

Lịch sử phát hiện ra luật

Tương tác của hai điện tích điểm theo định luật trên được Charles Coulomb chứng minh lần đầu tiên vào năm 1785. Nhà vật lý đã cố gắng chứng minh tính xác thực của định luật được xây dựng bằng cách sử dụng cân bằng xoắn, nguyên tắc hoạt động của nó cũng được trình bày trong bài báo.

Coulomb cũng chứng minh rằng không có điện tích bên trong một tụ điện hình cầu. Vì vậy, ông đã đi đến phát biểu rằng độ lớn của lực tĩnh điện có thể được thay đổi bằng cách thay đổi khoảng cách giữa các vật thể đang được xem xét.

Vì vậy, định luật Coulomb vẫn là định luật quan trọng nhất của tĩnh điện, trên cơ sở đó có nhiều khám phá vĩ đại nhất đã được thực hiện. Trong khuôn khổ bài viết này, các từ ngữ chính thức của luật đã được trình bày, cũng như các bộ phận cấu thành của nó đã được mô tả chi tiết.

Các bài tương tự: